Les modes couleurs indépendants : Lab, Lch, XYZ
Il existe plusieurs possibilités pour coder la couleur
Nous avons vu précédemment le RVB et le CMJN qui sont codés suivant des échelles allant:
De 0 à 255 pour le RVB (8 bits)
De 0 à 100 pour le CMJN (% d’encre)
De 000000 à FFFFFF L’hexadécimal pour le Web (RVB)
Il existe d’autres moyens de coder la couleur tel que:
Le TSL (Lch en anglais)
Le Lab
Le XYZ
L'avantage des modes Lab, TSL et XYZ, est qu'ils reposent sur la perception de l'oeil humain et que la description d'une couleur est précise et non dépendante à contrario des espaces RVB et CMJN.
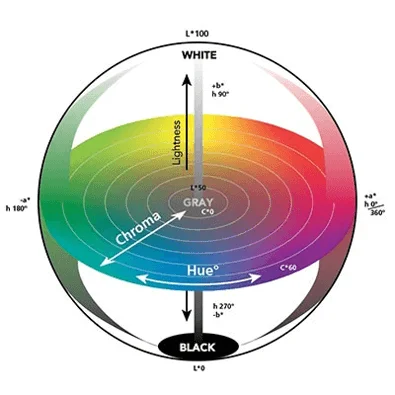
Le mode TSL (Teinte, Saturation, Lumière)
En anglais : Lch (Lightness, Chroma, Hue)
Le modèle TSL est un modèle colorimétrique perceptuel car il se rapproche fortement de la perception physiologique de la couleur par l'œil humain.
Dans ce système, les couleurs sont toujours caractérisées par trois dimensions mais qui ont une signification tout autre que dans le modèle RVB, puisqu'elles représentent ici la teinte, la saturation et la luminosité.
On représente généralement le modèle TSL à l'aide de deux cônes inversés placés l'un au-dessus de l'autre (figure ci-dessous).
- La teinte qui correspond à la perception de la couleur est mesurée sur une échelle circulaire (cercle de chromaticité de Newton) par un angle de 0° à 360°.
- La saturation mesure le degré de pureté d'une couleur, c'est-à-dire la quantité de gris ajoutée à la couleur. Elle est représentée par le rayon d'une section circulaire du cône et varie de 0% (niveau de gris correspondant) à 100% (couleur pure ou saturée).
- La luminosité représente le degré d'éclaircissement ou d'assombrissement d'une couleur.
Elle est définie selon une échelle linéaire allant de 0% (noir) à 100% (blanc) en passant par tous les niveaux de gris.
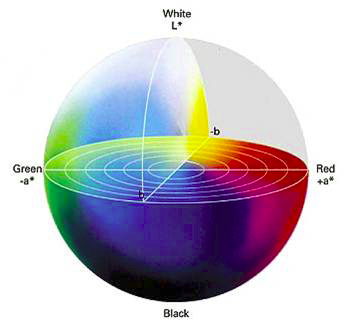
Le mode Lab
En 1976, la CIE (Commission internationale de l'éclairage) développe le modèle colorimétrique La*b* (aussi connu sous le nom de CIELab), dans lequel une couleur est repérée par trois valeurs :
- L, la lumière, exprimée en pourcentage représente l'axe des gris (0% pour le noir à 100% pour le blanc)
- a et b deux gammes de couleur allant respectivement du vert au rouge et du bleu au jaune avec des valeurs allant de -127 à +127.
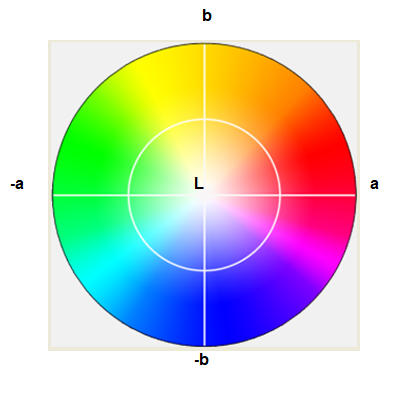
Le mode Lab couvre ainsi l'intégralité du spectre visible par l'oeil humain et le représente de manière uniforme.
Il permet donc de décrire l'ensemble des couleurs visibles indépendamment de toute technologie graphique.
De cette façon il comprend la totalité des couleurs RGB et CMYK, c'est la raison pour laquelle des logiciels tels que PhotoShop utilisent ce mode pour passer d'un modèle de représentation à un autre.
Les modèles de la CIE ne sont pas intuitifs, toutefois le fait de les utiliser garantit qu'une couleur créée selon ces modèles sera vue de la même façon par tous !
Le mode Lab est la passerelle entre les modes RVB et CMJN
Utilisé dans la gestion de la couleur et plus exactement dans les profils ICC.
Le modèle CIE XYZ
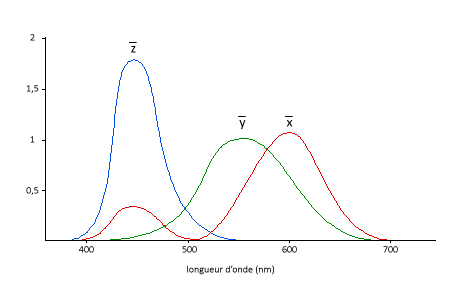
Le modèle CIE XYZ (également appelé modèle CIE 1931) est le premier modèle colorimétrique créé par la CIE en 1931. Réalisé à partir d'une série d'expériences sur la perception des couleurs par l'œil humain, ce modèle sert de référence pour définir d'autres modèles. Les trois composantes X, Y et Z du modèle représentent respectivement la teinte, la luminance (intensité lumineuse pondérée par la sensibilité spectrale de l'œil) et la saturation. Ces trois valeurs, dites valeurs tristimulus, qui sont fonctions du triplet lumière, objet, observateur, sont obtenues en intégrant sur le spectre visible le produit de la réflectance de l'objet éclairé par un illuminant par la sensibilité spectrale de l'œil humain (figure ci-dessous).
SENSIBILITÉ SPECTRALE DE L'ŒIL HUMAIN POUR UN OBSERVATEUR "STANDARD"
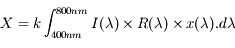
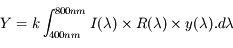
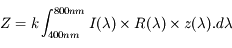
Avec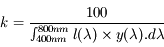
I: densité spectrale de l'illuminant
R : réflectance de l'objet
x, y et z : fonctions d'équivalence de couleurs
Le codage des couleurs